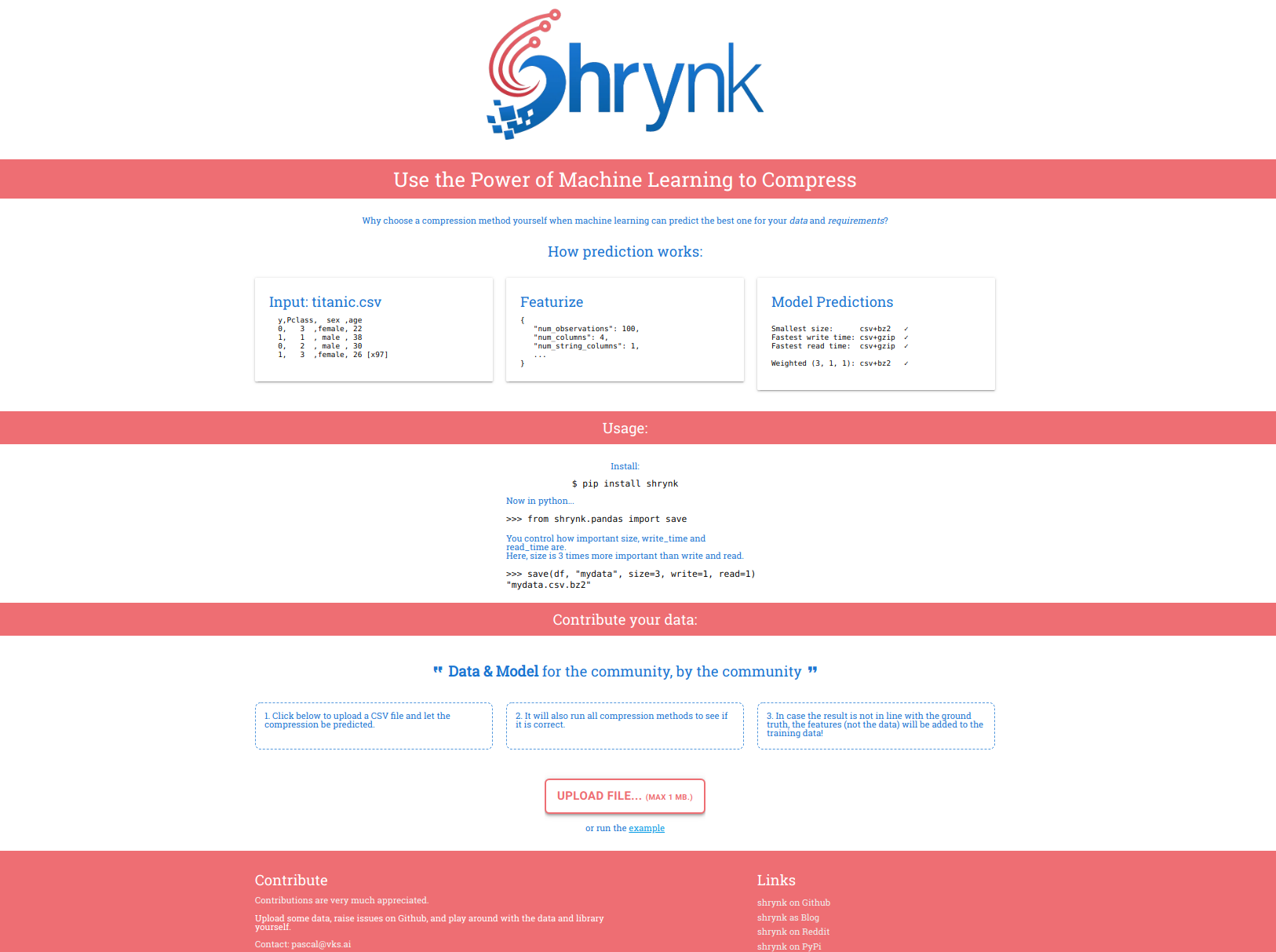
My server storing cryptocurrency data started to overflow as I was storing compressed CSV files. Trying to come up with a quick solution, I figured I should just switch to a more effective compression algorithm (it was stored using gzip). But how to quickly figure out which will be better?
Fast forward: I made the package shrynk for compression using machine learning! It helps you by choosing (and applying) the format to compress your dataframes, JSON, or actually, files in general.
Given example data, it is able to compress using 30% overall less disk space using a mixed strategy by machine learning compared to the best single compression algorithm (meaning: choosing any other single compression algorithm to compress everything will be worse).
You can try it for yourself at https://shrynk.ai.
Bonus: If the algorithm has it wrong, the features of the data (such as number of rows, number of columns, but not the data itself) will be added to the python package on the next release! This allows the algorithm to learn when to apply which compression algorithm.
Next, I will explain Compression, Machine Learning and the library I’ve built in Python. You can also jump to a section using the links below.
Compression
Compression is about reducing the size of data. The obvious reason for this is to be able to store more data. Since IO / Networking (to disk or over the internet) is often the bottleneck, and not CPU Processing, it makes sense to compress data before it goes in transit, and incur time for decompressing afterwards.
Different algorithms exist for different types of data, such as images, video, audio, but also text and general purpose files. Any data can be compressed as long as there is a pattern to use. For example, a compression algorithm might find that in images there is a lot of repetition: there will be areas of pixels with the same color, and it is possible to use compression to avoid having to store every single pixel invidivually.
In video, it is not just “2D” but there’s a time dimension as well, and one succesful way to compress might be to only store the delta between frames, that is, only store where the video is different from the last frame. Yet another example is whitespace which can be compressed in JSON files.
Compressing tabular data
The first case of shrynk has to do with matrix/tabular data: rows and columns of data. Here is an example file called toy_data.csv:
gender,age
female, 20
female, 30
female, 40
male, 50
male, 60
Let’s concern ourselves with the gender variable only. For each row, storing female or male is not optimal given that we know these are the only values in this column. One improvement could be to take all the values in the column, and doing a replacement: F for female, and M for male. The shorter the string, the better, right? Of course, to decompress you need to add the extra data that F means female, and M means male, but like this you only have to store the “longer” string once. This is a part of what is called dictionary encoding and is used in the Parquet format.
Another optimization of Parquet is to use Run-length encoding, which makes use of the observation that very often the same value occurs in sequence. Oversimplifying a bit, we could encode the column gender as 3F2M. Decompressing this would expand it back into the original data.
Note that at the same time, you might be able to imagine that the Parquet schema is not necessarily better for floating-point values (like pi), as mostly these values will be unique, we cannot use these tricks.
Tabular data in Python
In the case of tabular data, we often use pandas.read_csv to read in data from disk and produce a DataFrame.
However, csv is often uncompressed. A dataframe can easily be written back to disk using compression though. Here are several available options, with and without compression:
fastparquet+UNCOMPRESSED
fastparquet+GZIP
fastparquet+SNAPPY
fastparquet+LZO
fastparquet+LZ4
fastparquet+ZSTD
pyarrow+brotli
pyarrow+gzip
pyarrow+lz4
pyarrow+snappy
pyarrow+zstd
csv+gzip
csv+bz2
csv+zip
csv+xz
csv
The first part before the + is the “engine” (csv is handled by df.to_csv, and pyarrow and fastparquet are different libraries used for df.to_parquet), whereas the latter part is the compression that is being used.
It turns out that it is difficult to find out when to use which format, that is, finding the right “boundaries” choosing between so many options. It depends on a lot of factors.
It would be great to know which compression would be best, wouldn’t it?
Running benchmarks
First of all, shrynk can help with running benchmark for your own file, or of course, for a collection of files.
I took the gender / age toy data from before and show below how to get the actual profiled results per compression for a file.
from shrynk import show_benchmark
show_benchmark("toy_data.csv") # takes either a(n un)compressed filename, or DataFrame/object
# Output (sorted on size)
kwargs size write read
csv+bz2 87 0.135 0.138
csv 89 0.136 0.139
csv+gzip 97 0.137 0.140
csv+xz 112 0.140 0.143
csv+zip 218 0.133 0.137
fastparquet+LZ4 515 0.277 0.279
fastparquet+GZIP 518 0.284 0.286
fastparquet+SNA.. 520 0.295 0.298
fastparquet+ZSTD 522 0.273 0.275
fastparquet+LZO 526 0.281 0.284
fastparquet+UNC.. 556 0.438 0.675
pyarrow+brotli 1146 0.016 0.023
pyarrow+lz4 1152 0.015 0.018
pyarrow+snappy 1171 0.012 0.016
pyarrow+zstd 1180 0.013 0.018
pyarrow+gzip 1209 0.017 0.023
You can see that in the case of this file, it is recommend to store the data as csv+bz2, as it yields a very small file on disk (and it uses the default settings).
Running all the compression benchmarks only took 3 seconds on my laptop, which might make you wonder why we wouldn’t just always run the benchmarks? Well, for any sizeable dataframe, you do not want to have to run the benchmarks as this can take a very long time - especially for an unfortunate compression algorithm taking a long time for the particular data at hand. At the same time, why run the benchmarks when we can predict? Enter Machine Learning.
Machine Learning
Computers are good at automating human decisions. In order to make decisions without having to explicitly program it to do so, it will instead leverage historical data, such as characteristics and actual decisions, to predict the best decision in the future for new characteristics.
For example, Machine Learning helps in deciding whether a new email is spam based on users having labeled loads of other emails in the past as either spam or not spam (the decisions), and using the words (their characteristics) that occur more frequently in the spam emails (e.g. “Nigerian Prince”) opposed to the non-spam emails (e.g. “Hi John”) to drive the decision. Well, assuming that the person’s name was actually John, of course, otherwise it’s probably spam again.
The usual downside of machine learning is that it is very costly to gather the correct decisions - it is often manual labor by people.
The cool thing about machine learning for compression is that we can try all compressions for a file to find out what the optimal decision would be, without much cost (except time).
In this case, ~3000 files have been used to allow the modelling of the compression. Their characteristics have been recorded and the things we would like to learn to minimize:
-
how large they become (
sizeon disk), -
how long a write takes (
write time) and -
how long a read takes (
read time)
It could be that, based on some data of let’s say 5000 rows and 10 columns of price data, compression A is best in terms of size, but if it concerns 500 rows and 100 columns of time data, compression B would be best. Perhaps depending on other factors, such as the amount of text columns, the situation will again be different.
To give more example features, currently it will consider percentage of null values, average string length, and how distinct variables are (cardinality), and even a few more. These are all used to figure out which compression to apply in a similar context. Check here for an overview of features used.
Machine Learning in Shrynk
Note that there are other attempts at using machine learning to do compression… most notably in compressing images. Shrynk uses a meta approach instead, as it only uses already existing compression methods.
For each file, it will apply the compression and gather the values for each compression algorithm on size, write and read columns and converts them to z-scores: this makes them comparable at each dimension and is a novel approach as far as I know. The lowest sum of z-scores given the user weights gets chosen as a classification label. Let’s see that in slow-motion.
First to see how converting to z-scores works:
from sklearn.preprocessing import scale
scale([1, 2, 3])
# array([-1.224, 0, 1.224])
scale([100, 200, 300])
# array([-1.224, 0, 1.224])
You can see that the scale does not matter but the relative difference does: (1, 2, 3) and (100, 200, 300) get the same scores even though they are 100x larger. Also note that here we are ignoring the unit (bytes vs seconds).
Here a fake example to show 3 compression scores of a single imaginary file, and only considering size and write:
size write
compr A 100kb 2s
compr B 200kb 1s
compr C 300kb 3s
Converting per column to Z-scores:
z-size z-write
comp A -1.22 0
comp B 0 -1.22
comp C 1.22 1.22
Then to multiply the z-scores with User weights (Size=1, Write=2):
u-s u-w | user-z-sum
-1.22 0 | -1.22
0 -2.44 | -2.44
1.22 2.44 | 3.66
In the last column you can see the sum over the rows to get a weighted z-score for each compression.
Given the example data and s=1 and w=2, compression B would have the lowest summed z-score and thus be best! This means that the characteristics of this data (such as num_rows etc) and the label compression B will be used to train a classification model.
In the end, the input will be this result for each file (so the sample size is number_of_files; not number_of_files * number_of_compression).
A sample data set might look like (completely made up):
num_cols num_rows missing | best_label
19 1000 0.1 | csv+bz
5 10000 0 | fastparquet+GZIP
55 2333 0.2 | pyarrow+brotli
190 500 0.05 | csv+gzip
... and so on ....
A simple RandomForestClassifier will be trained on the included benchmark data for 3000 files, based on the user weights.
Knowing that, let’s look at some usage examples.
Usage
Basic example of saving (which predicts the best type) and loading:
import pandas as pd
from shrynk import save, load
# save dataframe compressed
my_df = pd.DataFrame({"a": [1]})
file_path = save(my_df, "mypath.csv")
# e.g. mypath.csv.bz2
# load compressed file
loaded_df = load(file_path)
If you just want the prediction, you can also use infer:
import pandas as pd
from shrynk import infer
infer(pd.DataFrame({"a": [1]}))
# {"engine": "csv", "compression": "bz2"}
For more control, it is possible to use shrynk classes directly:
import pandas as pd
from shrynk import PandasCompressor
df = pd.DataFrame({"a": [1,2,3]})
pdc = PandasCompressor()
pdc.train_model(3, 1, 1)
pdc.predict(df)
pdc.show_benchmark(df, 3, 1, 1)
After installing it is also available on the command as shrynk.
Use it to automagically compress, decompress and run benchmarks for files:
shrynk compress mydata.csv
shrynk decompress mydata.json.gz
shrynk benchmark mydata.png
Data comes packaged
Note that the data comes packaged in shrynk: this is a feature, not a bug. It allows people to provide their own requirements for size, write and read speeds. It will then train a model on the spot (if not trained earlier).
I also hope that including the data encourages others to see if they can improve the compression score :)
You can also use it for validating improvements to the algorithm, or generically, the approach.
How well does it work? Cross-validation
I have builtin a validate function that is available to all shrynk classes so you can test your own strategies or train and verify results on your own data.
It uses the available data for the given class, and produces results for cross-validation; taking into account the user defined weights.
Validation was a tough one, mostly because it took me a while to figure out how to express the results in a meaningful way when allowing the use of weights. In the end I chose to keep the dimensions of interest, size, read, write, and show how the aggregate of shrynk’s predictions per object compare (in proportions) against choosing to always use a single strategy. I hope the example makes it clear.
See the code below:
from shrynk import PandasCompressor
pdc = PandasCompressor()
weights = (1, 0, 0)
acc, result = pdc.validate(*weights)
Note that shrynk in the example below is not only 31% better in size (check the arrows), but also much better in terms of read- and write time compared to always applying the single best strategy, csv+xz.
The 1.001 value indicates it is only 0.1% away from what would be achievable in terms of size if it would always choose the best compression per file in the validation set. At the same time, it is 6.653 times slower in terms of reading time compared to always choosing the best. It was after all optimizing for size.
[shrynk] s=1 w=0 r=0
----------------
it 0/5: accuracy shrynk 82.49%
it 1/5: accuracy shrynk 100.0%
it 2/5: accuracy shrynk 78.88%
it 3/5: accuracy shrynk 83.33%
it 4/5: accuracy shrynk 99.95%
Avg Accuracy: 0.889
results sorted on SIZE, shown in proportion increase vs ground truth best
size read write
shrynk ---> 1.001 6.653 7.443
csv+xz ---> 1.311 25.180 31.659
csv+bz2 1.370 12.698 14.549
csv+zip 2.163 11.646 13.701
fastparquet+ZSTD 4.845 5.069 6.625
fastparquet+GZIP 4.958 6.866 8.805
fastparquet+LZO 5.666 4.959 6.446
fastparquet+LZ4 5.858 4.874 6.395
fastparquet+SNA. 6.008 5.105 6.611
csv 7.454 9.214 10.663
csv+gzip 7.455 9.114 10.543
pyarrow+brotli 8.418 2.163 3.045
pyarrow+zstd 8.715 1.219 1.495
pyarrow+gzip 9.044 2.038 2.864
pyarrow+lz4 9.320 1.126 1.366
pyarrow+snappy 9.356 1.165 1.433
fastparquet+UNC 16.360 5.851 6.870
Lastly, let’s look at user weights of size=3 and write=1 to see a mixed approach:
size write z
shrynk 1.422 4.069 -4.258
csv+bz2 1.330 9.621 -3.139
csv+zip 2.148 7.857 -3.063
fastparquet+ZSTD 6.149 6.379 -1.183
fastparquet+GZIP 6.239 7.307 -0.939
fastparquet+LZO 6.968 6.470 -0.716
fastparquet+LZ4 7.035 6.424 -0.689
csv+xz 1.272 22.527 -0.452
fastparquet+SNA. 7.564 6.481 -0.387
pyarrow+zstd 10.790 1.453 0.320
pyarrow+brotli 10.400 2.806 0.391
pyarrow+lz4 11.323 1.307 0.581
pyarrow+snappy 11.365 1.338 0.610
pyarrow+gzip 11.147 2.469 0.729
csv+gzip 11.243 6.598 1.652
csv 11.263 6.564 1.655
fastparquet+UNC 24.420 6.694 8.887
Conclusion
Since having to come up with manual rules for when to use which compression would be very complex and time costly, this was a great case for machine learning. It’s very scalable, as when a new compression algorithm shows up on the market, shrynk will be able to benchmark that one and no new rules have to be figured out.
Note that it currently required 30% less disk compared to if I would have used only a single best strategy (in reality, you might not even always use the single best strategy but a worse one). Though, granted, this was on rather heterogeneous data: small, big, and really versatile, e.g. in terms of text, and missingness. To prevent bias, it was trained on balancing the occurence of all compression algorithms to be best.
You know you’re in for a win with machine learning when you can get (or even create) data cheaply.
It also illustrates an awesome way to enhance coding: by having a computer predict the best way to do “something” - in this case, compress.
What’s next
If you’ve liked this, feel free to follow me on github and leave a star for shrynk on github.
If you haven’t tried it yet, you can see what it looks like in action at https://shrynk.ai
And please help out if you’re interested, as any attempts at Pull Requests will be welcomed: it’s a python project, by the community, for the community.
- Further investigation of which variables are most predictive (and cheap to compute)
- The stats computation could probably be sped up as well once we further investigate which features are most succesful.
- Add other data types to the framework (JSON and Bytes have recently been added)
- I’ve been working on a package to generate artificial data. Imagine creating slight variations based off requirements, or existing dataframes to have data evolve in the direction we want to learn better boundaries!
- Other improvements?